(一) 半个月前去比利时参加了公司的 end-of-year party。我在回程的火车上翻看和组里同事的照片以及群里过去一年里正经又不正经的聊天记录,不禁在脑海里哼唱起了 Maroon 5 的 Memories: "Cause the drinks bring back all the memories... Of everything we have been through"。然后,就在接下来的两天里利用空余时间赶了一个纪念2024年的小视频,用了这首我不禁想起的歌做背景音乐。 在播视频之前,我不想要给大家过高的期待,便铺垫到:“如果单从技术水准和艺术性来说的话,应该随便找一个靠谱的AI软件都要比我用 imovie 做了几个小时的成果要好很多;但是从故事性来说,我相信自己还是更胜一筹的。” 老板回答说:“Yeah, because AI doesn't have the context." 是啊。Our context; our memories. 就算把这一年所有的照片和聊天记录都丢给一个模型,它所得到的 input 都远不及那个在电脑前笨手笨脚、东拼西凑的我。它没有经历过那些匆忙的日日夜夜,更没有参与过那些晚餐时的灵魂问答。就算把生活中的所有琐碎与对话都记录下来,转换成模型可以辨识的格式当作 input,那它也会错过那些时刻中大家的表情、心绪和情感吧。也许有人会说,思绪和情感无非是场景和对话下的 output 罢了,是可以用模型来模拟的;我不完全反对这个观点,可即使这个模型能够生效,它也大概需要每个人过去的所见所闻、所思所感作为 input 吧。 The context relies on old memories, and it shapes new memories....
想说给五年后的自己
引 过去一个月在断断续续地追《平凡之路》,昨晚看到了结局,其中一句话让我印象深刻:“永远不要成为自己年轻时所鄙视过的人,也永远不要把这个世界让给自己所不齿的人。”可问题来了,同时做到上半句与下半句的几率有多大呢?真的可以在“征服这个世界”的过程中做到洁身自好、不被年轻时的自己所鄙视嘛? 问题一:为什么要在意是否被年轻时的自己所鄙视呢? 记得在高中的时候也和好友讨论过类似的问题,他当时的回答大概是“这不重要”。毕竟一个人在成长的过程中,价值观的改变是必然也是必要的。只要每一时刻自己的想法和行为是自洽的,就不必在意从前的自己的评价。我们暂且假设“自洽”的这个前提是成立的,即当你在未来的某个时间点做了年轻时自己所鄙视的事情时,你的价值观就已经发生了改变,也就是说,曾经鄙视的事情已经被自己接受和认可。他的这个解释要成立还有另外一个潜在的前提:在评判自己行为好坏的时候,要以当下的价值观为衡量标准,以前的不算数。也就是说,recency trumps --- 好像也不是完全地在推卸责任,毕竟我们购买商品的时候不会用十年前的物价来衡量贵贱,为何要在道德评判这个层面揪着过往不放呢? 问题二:为什么我们道德的潜意识里会要以年轻时自己的想法为标杆呢? 当我们更看重自己年轻时的想法时,我们其实在潜意识里有一把道德的标尺,一端为好,一端为坏。假设计量单位是“坏值”,好端为零点,坏端为百点,做与不做的边界是十点,鄙视与不鄙视的边界是二十点。年轻时的自己在决策时有个条件运算式:if 0<=x<=10, 好事会去做;if 10<x<=20, 不会去做,但他人做了也不鄙视;if x>=20,坏事不会去做,他人做了会心生鄙夷之情(注:x为一件事情的“坏值”,这里假使这是个客观存在的值)。那么,当我们若干年之后做了一件x>20的事情时,我们现今所做的事情的最大“坏值”大于年轻时(假使年轻时的自己严格遵守当时的条件运算式),不论当今的自己的条件运算式变成了什么样,这本质上都是离坏端更近了一步,也就是我们平时所说的“道德的滑坡”。因此,先前的这句话也不是要奉年轻时的自己为标杆,只是说,不要增加所做的事情的“坏值”而已。那么问题来了,道德真的有标尺吗?这个标尺真的只有一个维度吗?以及每件事情真的有其本身且固定不变的“坏值”吗? 问题三:如何衡量道德? 【打完上面这句话,心里第一个想法是:噫,你竟妄想回答这个问题?快想想怎么逃避它...】 我认为,世界上大多数人(包括我在内)是相信有善恶之分的,不过道德好像真的很难从一个固定的维度去衡量。甚至说,衡量(非自我的)道德本身好像就是一件不那么道德的事。借用之前读到的一句话:不经他人苦,莫劝他人善。先不说这句话能否给我们提供衡量道德的线索,它至少可以被理解为:鄙视或是衡量本身就是不被允许的。这里的”他人“既包括除了自己以外的人,也包括那个未来的自己(毕竟年轻的自己没有经历过现在的自己的苦,现在的自己也无法经历未来的自己的苦)。 【那么,关于过去和现在的自己呢?暂时是真的无解了,就先用“道可道,非常道”来蒙混过这篇小作文吧....】 结 写这篇文章的初衷是因为在《平凡之路》的这句话中听出了一丝共鸣吧。关于后半句:我从未掩饰自己的野心,和老板们讲,中国有句古话,“不想当将军的士兵不是好的士兵”。关于前半句:前两周,我和现在的老板一对一聊天,他大概的意思是,“executive一项很重要的职责是build organizational alignment,你现在非常黑白分明,接下来几年要锻炼的是去理解每个人在不同位置上的苦衷,然后想到折中甚至妥协的解决办法。“ 我还是很感激和接受他这个评价的,不过在当时的我看来,这条路有三个级别:1) understand and accept others as who they are; 2) build alignment and tag them along to achieve the common goal; 3) maintain your own moral compass while doing the first two steps。...
最难过的是无能为力
最难过的是我在你的身边,但你的难过与我不尽相关。我只能无力地安慰,却始终触碰不到你的心,给不到你想要的。 所谓思念,就是再无聊的事情,两个人一起也会开开心心;再有意思的事情,一个人也内心毫无波澜。
边缘性虚无主义
今天跟管老板聊到虚无主义,他说我可能是个虚无主义丧B,于是推荐我去看一个虚无主义自救的视频。 大概来说,虚无主义就是觉得生活中各种事情都毫无意义,也许甚至连活着本身也毫无意义。吃了老板安利我去看了那个视频,最后的结论是我应该不是一个虚无主义,只是时常觉得自己做的事情不管是工作还是活动没啥意思罢了,更多的是对现状的不满。没有意思和没有意义,我认为有这天壤之别。但是同时,时常觉得很多事情新鲜感过去之后变得没有意思这件事情,跟虚无主义也确实有所关联但程度略有不同,我在下面会详细表示。 回到虚无主义,今天看的视频大概提到了哲学家们对“虚无感”的来源的几种解释,以及它们各自认为的对抗虚无的方式。我在这里总结一下: 以下是我从视频内容总结出来的理解,因为没有亲自看过这些哲学家的书,所以下面的内容至少算是三手信息。 克尔郭凯尔 克尔郭凯尔认为,极致追求理性的结果是忽略了个体特性,于是发现有些理性推导出来的结论对自己也许没有那么适用或者自己并不喜欢。于是如果纯粹的理性并不适用,那么也许走出虚无的解决方法就是回归自己本心,寻找自己最感性的那一面所追求的东西。这个东西不需要说得明白,也不需要是理性的,是不需要justify的,只是自己相信认同的。这样的东西统称为信仰。如果这种信仰足够encompassing,足够你依照信仰去做大部分重要的决定,那么虚无感就会消失。宗教是信仰的一种。作为一种普适信仰,宗教便是通过这样的方式去让人走出虚无的。 叔本华 叔本华认为,虚无来自于无尽的欲望。人总有各种各样的欲望让你不断去追寻,得到之后感到空虚又不断去追求新的欲望。这些欲望最本质的来源也许是对来自于对“生”的渴望。不论仅仅是为了活下去,还是为了活得更好(也许希望活得更好是对活下去的一种保险机制),这种渴望是自然的也是盲目的,并且所有的生物都被这样的本能所驱使。但是放弃对“生”的渴望又是错误的解决方法,因为这只是对“生”的渴望的一种屈服。We must fight, 通过禁欲来反抗。 尼采 尼采认为人固然被“生”的意志所驱使,但是大多数现代人尤其是物质资源相对丰富的人群仍然会感到空虚,这不是仅仅用被“生”的意志驱使所能解释的。尼采认为人还渴望“生命的释放”,应该大概是类似于马斯洛说的自我实现。几乎所有的宗教信仰都会描绘一个美好的彼岸,于是信仰宗教的人们愿意为了那个彼岸而努力,不会觉得在此生所做的事情是没有意义的。但是“彼岸”的问题在于,这是一种间接的救赎,但是人本可以过好此生,让此生的生命得到释放,而不需要寄托于一个虚幻的彼岸,所以宗教(甚至广义上的信仰)都不是对抗虚无的正确方式。正确的做法是打破一切虚妄,努力创造价值去打破虚无(没有什么实际指导意义)。 萨特 萨特认为人感受到的虚无来自于人的一个特殊性,就是人是自由的。如果有目标有目的那么自然就不会感到迷茫和虚无。蜜蜂不会感到虚无因为它们生来就处于本能有需要做的事情,无论来自基因还是来自母蜂/社群的教导,他们打心底里接受了,就不迷茫也不感到虚无了。但是人不同,人太自由了,有很强的主观能动性,可以做各种各样的事情可以成为各种各样的人,于是会迷茫,于是会感到虚无。所以虚无感是正常的。无论是选择宗教信仰还是选择断绝欲望,那都是对自由所带来的虚无感到恐惧而逃避的做法。所以真正断绝虚无的做法就是接受虚无,并且积极主动地去创造自己生活的意义,这意味着不停走出自己的舒适圈(在舒适圈内过于舒适,得其所得之下的虚无)。 加缪 加缪认为,虚无感来自于一种荒谬感。荒谬感的产生是因为世界本无意义,而我们作为人却不停地在寻找意义却又找不到。这就让我们觉得自身和这个世界产生了深深的隔离感。这让我们痛苦,因为好像每天日复一日在做一些重复却没有意义的事情。加缪提出的解决办法就是活在当下。他认为世界本没有意义,去强行寻找意义思考意义才是这种荒谬感的来源,也是虚无的来源。那么最好做法就是接受无意义,转而去感受生活本身。 我自己的想法比较偏向萨特。对克尔凯郭尔的解决方案,我认为如果都从盲目的信仰出发,完全依托信仰做决定,那这是一种偷懒和不负责任的行为。对叔本华,我认为禁欲同自杀一样,也是对虚无的屈服。人要接受自己有不断产生的欲望,并manage it。对尼采,观点基本同意,但是不太具备指导意义。对加缪,如果意义对我很重要,那么即使承受虚无的痛苦,也会想寻找意义。活在当下听着没错,但似乎总觉着差点意思。对萨特,有时候即使想法到了,但是在执行上还是会有因为状态和心情很难去做出调整。这些哲学家的观点基本都从自身出发,但是也许很多时候一个人自身会很无力的,对抗虚无,未必需要一个人。
写在2022年的最后一天
(一) 前两天去学校附近的雪板店,想着要不要换一个新的雪板。现在的雪板大概用了一年左右,还是蛮耐用的,只是滑起来的时候总觉得它不是最合适的。刚买回来就觉得它有点大了,但当时心想着刚刚入门就勉强凑合一下,现在遇到了一些动作上的瓶颈,就不自觉地开始找各方面的原因。 讲道理,无论是按照身高还是体重来比对,这个板的长度和宽度都比最适合我的尺寸要大一点点,但又没有大到离谱的程度。我拿着现有的雪板和卖板的小哥说自己现在的换刃总是做不到很丝滑,想要换个小一点点的板子。谁曾想,小哥的答复居然是:“以你现在的水平,换个小点的板子自然是会让你滑得更顺,但是你手里的这个雪板会帮你提高地更快。” 说他“一语惊醒梦中人”似乎有点夸张,但还是有种被教育和点醒的感觉。所以,我们滑雪的目的究竟是什么?而这些器具与我们之间又有着或是该有着怎样的关系呢?板子可以不只一个,可每段路,我们只能用一个。舒适和历练是道单选题。有趣的是,有时候也很难判断哪条路是舒适,哪条路又是历练呢。 (二) 今天是2022年的最后一天,早上醒来之后思考这一年与之前最大的不同在哪里,脑海中浮现的第一个词语是“孤独”。现代的社会似乎很习惯赋予“孤独”负面的色彩 --- 你若是和朋友说自己孤独,别人的第一反应往往是“那我们怎么能让你感到不那么孤独呢?”直到前两周,我的房东小姐姐(也算是我在犹他结识的最好的朋友)和我讲:”你确实过得比身边的大多数人都孤独,但我觉得你是一个能够享受孤独的人。“ 这个月月初见了坡党的一个学长,我们在叙旧的时候,他提到了一个词语“集体生活”。我觉得这个词真的是可以很精炼地总结我出国前十年(2011-2021)的生活状态,也道出了这一年与从前的不同。在之前的十年里,虽然我们离开了父母和熟悉的环境,辗转于不同的国家和城市,可是身边总是有一群生活背景与人生阶段类似的朋友。即使是毕业走入职场,周围也少不了高中和大学小伙伴们的陪伴,过得依然像学生时代一样。 这一年的生活状态就很不一样,身边没有固定的朋友圈,也没有固定的可以一起出去吃喝玩乐的朋友。当周围的人积极地参加各种聚会的时候,我会刻意地去选择避开大多数喧嚣热闹的场合,也会刻意地在每周都保有足够多和自己单独相处的时间。当然,我也不是完全地自闭,这种方式反而让我有更多和喜欢的朋友一对一的时间,也让我有更多的时间去消化和反思经历的事情。这学期快结束的时候,我提议和一门课上的组员们做group debrief,本意是让大家开诚布公地互相提建议,可最后说着说着,他们就开始感慨这一学期都没怎么和同组的组员有除了课业之外的交流 --- 出乎我意料的是,他们又不约而同地接着说:”在这个组里,好像这学期也就和梓钰有过比较私人的交流。“ 我一边想着自己anti-social的人设就要这么崩塌了嘛,一边还是有点小小的安慰吧。 孤独是一种境遇,也是一种心态。境遇在于身边的大多数人确实处于人生的不同阶段,我也不愿意去更有效率地结交更多的人。心态则在于,无论是与他人的界限,还是和自己的独处,都是现在的我十分看重的东西。当然,孤独也不会常常都让人感到自足与平和,恋旧或感伤的体验,就都当作是成长和修行吧。 (三) 我们学校的圣诞假期往往是两周,唯独今年是三周。说实话,现在两周过去了,我还是挺希望能快点去上学和上班的。倒也不是假期过得不开心,而是有种放松够了又满血复活的感觉,我昨天便真的忍不住去公司上班了。 之前在咨询公司的时候,我曾经调侃说自己的工作就像做作业、检查作业和交作业的过程。每个项目都有一个八九不离十的scope,我们只需要给出证据确凿、逻辑缜密并让客户满意的答案就好。在公司工作嘛,感觉就完全不一样,得出结论的过程自然也需要证据确凿和逻辑缜密,但是答案怎么说就是一门艺术了。和咨询工作不一样,答案本身不是结果,目的是让公司其他人听了之后有所行动。在公司里很多时候的工作其实是给自己和不同部门的老板们留作业,而为什么老板们要花时间做你留的作业又是一门艺术了。 刚刚发现很有趣的一点,我2022年最后做的工作是和乙方制作团队就customer focus group的后期视频剪裁对接,而2023年的第一个会议是和公司宣传部门商讨明年的对内宣传策略。虽然我自认为工作的大部分时间是和搞数据分析的人对接,但好像不知不觉中也不得不和搞内容创作的人保持非常紧密的联系。 来美国这一年多的时间,身边有同学同事说我是个非常擅长讲故事的人,也有朋友提出相反的看法,觉得我过于依赖hard facts,而不懂得去欣赏说话之道的价值。这些评价也让我去反思对讲故事这项技能本身的看法,以及对自己未来的规划和定位。怎么说呢,我真心觉得,能讲好故事是有力量的,也是令人敬畏的。可正因如此,它也是一把双刃剑 --- 用准了地方,事半功倍;可若是掺了些不纯的私欲和杂念,那便成了蛊惑人心的伎俩了。
碎碎念
最近网上有许多关于美国最高法院从宪法中移除终止妊娠权的讨论。也许是因为出生成长在独生子女政策的时代,我很长一段时间都没有觉得人流堕胎是值得争议的一件事情。甚至记得小时候,哈尔滨公交车上面车载电视的广告很多都是关于无痛人流的 --- 因此留下的印象便是:人流不过是一种正常的手术,和分娩并列在产科下面;它和其他科室那些切除手术本质也没啥区别,不过是利用科学的手段移除体内“undesirable"的部分而已。 想想有些滑稽,西方世界批评中国的独生子女政策不尊重自由选择生育的权利,可这个政策又使得女性的终止妊娠权变得天经地义。当然也有些无奈,鱼和熊掌难以兼得,在许多体制下面,自由生育的权利和自由终止妊娠的权利不能两全 --- 多么矛盾的一件事情呀:如果你赋予了别人A的自由,却又限制其not A的选择,这在本质上不就是颠覆了自由的定义嘛。 我很少对政治政策评头论足 --- 遇到诸如此类的新闻,我自然是有情感方面正面或负面的触动,可是与其说从道义上支持或反对某个政策,我往往看到的只是个人价值和社会利益的冲突 (与此同时,个人价值在很多方面依附于社会利益)。当然,以这个新闻为例,关于要更注重孕妇还是胎儿的个体权利,移除终止妊娠权是否真的能带来实际的社会利益等等,这些本身就是值得争议的话题。可是跳出这个背景来看,有一点是通用的,个人在享受一个社会群体带来的福利时,就是要付出一些牺牲和代价的,说得高大上一些,可能就是所谓的契约关系吧。从大刀阔斧的政治改革到翻来覆去的政策修订,只要不是完全用来满足独裁者的私欲,无非就是在各种真假难辨的假设下,寻找一个local optimum而已。而每个个体对于政策的争辩,也往往只是站在自己的角度罢了。 这样的想法还蛮悲观的,因为它好像贬低或是降低了所有改革和改变的宏观意义。有时就是要大胆地去相信那些真假难辨的假设,去发声和争取,才能换来社会的发展和进步吧。可社会的发展和进步听起来也有些虚空,也许真正的价值在于个体发声和争取的过程。倘若连发声和争取的权利都没有呢,那能去有意识地相信一些真假难辨的假设,并有情感的共鸣,也好歹算是真真正正地活过吧。这要求,也是真够低的了。
最近公司股价暴跌之后的一些想法
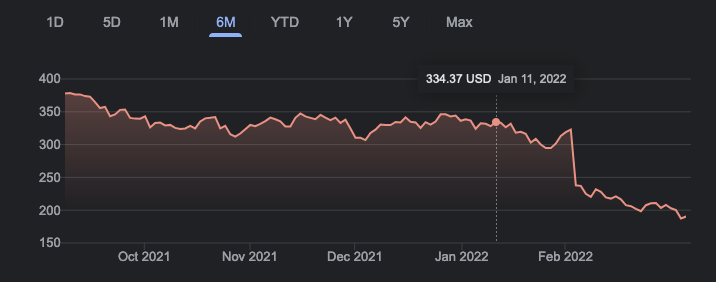
今年二月初公司发完财报(去年Q4的财报)以及今年Q1的盈利预期,盘后公司股票暴跌25%。 再加上这段时间对美联储应对通胀会采取的加息的预期,以及俄罗斯乌克兰打仗,几件事情下来公司股票已经officially从历史最高价腰斩。客观来讲,Facebook Q4财报数据其实还不错,整体营收增长,以及几乎所有地区的per user收入增长。如果不考虑机构砸盘的操作,盘后股价暴跌的主要原因主要来源于公司的增长预期不好, 毕竟公司市值基本上等于当前实际价值乘以PE ratio,PE ratio则正比于未来potential的成长倍数。增长预期不好,简单来说就下面这么几点: 1. 用户增长停滞 (Facebook family apps已经达到每日近30亿日活,要再增长真的很难) 2. 受到抖音的冲击比较大 (用户在产品上花的时间被分走) 3. 对标抖音的短视频产品暂时没什么营收,且营收效率会远远低于传统的feed营收 (这个也没办法,产品形态决定了, 而且初期也不可能疯狂投广告) 4. 公司预计在Reality Lab/元宇宙上砸重金 (超级超级高的成本,近千亿美元一年)。 当然近期也不只是Facebook股价暴跌了,基本上整个纳斯达克都崩盘。不过有一说一,Facebook崩得确实最厉害。不知道市场的consensus是怎么样的,似乎都不是很看好做metaverse这件事情。不过小扎一直都是一个很坚定自己的决定,就想做自己想做的东西的这么一个人。在公司财务还可以的状况下,不管外界怎么说,都不大可能动摇他的决心。这点上我很佩服他。Metaverse这个东西,我对其目前的理解可能还比较粗浅。在我看来metaverse只是把现存的几个分散的概念给整合起来的一个结合点。从practical的角度来说,没有觉得会有多大的实质性改变。这边说的分散概念主要是指基于区块链/NFT技术的虚拟asset(有虚拟asset的概念就可以有效交易,从而建立经济体系)、基于AR/VR的交互层,以及用于优化体验的AI相关技术。元宇宙算是这几样相对零散的技术领域的一个比较natural的交汇点。从技术的应用角度来说是这样子。从产品的角度来说,现在各种各样的互联网产品已经占据了用户绝大部分的时间,那么当用户价值无法从时间这个维度被继续exploit的时候,很自然的我们就想去拓展空间这个维度去继续exploit用户价值。从技术可行性的角度来说,扩展虚拟空间显然比利用物理空间甚至拓展物理空间更加容易,而且一片蓝海。这几个因素结合之下,出现元宇宙这个概念也是很自然的一件事情。 任何相对比较新的概念在出现的初期肯定是会受到争议的。争议的来源之一就是大家对这个新概念的定义还没有共识。你认为元宇宙是这样的,我认为元宇宙是那样的,而他的想法又与我们都不相同。我不知道小扎对元宇宙的最终形态是否有想法,但是不论是迫于资源限制又或者是自己坚定的信念,Facebook版本的元宇宙在初期形态会把AR/VR设备作为入口点。这也是用户接触元宇宙的portal。除了小扎版本的元宇宙,less aggressive的元宇宙形态可能更像是Roblox和Decentraland之类的将Web2.0和Web1.0设备(手机、电脑等)作为入口点那种,也可能是更aggressive的Neuralink那种直接在未来用脑机接口接入的那种(这只是我的想法,毕竟Neuralink没说自己要做元宇宙产品)。从我现有的认知来看,Web1.0和Web2.0接口的元宇宙虽然也可以实现虚拟经济,也算是拓展了虚拟空间,但是不具有颠覆性的体验,无法吸引足够多的人加入,最多是个非常早期的过渡阶段的产品。基于脑机接口的元宇宙则碍于technology readiness也许过于长远。相比之下基于AR/VR的元宇宙概念是我最认同的,至少在未来5-10年内会存在的一种元宇宙形态。 抛开对元宇宙vision的讨论,元宇宙作为一个虚拟世界也会对这个现实世界产生影响。会有正面影响,也会有负面影响,那么随之而来的也会存在ethical的问题 (插句题外话, 不怕被骂,我个人其实一直以来都不是特别care各种ethical的问题。不管是AI技术的ethical问题,还是克隆技术的ethical问题,还是privacy相关的ethical问题,都统统不care。在选择自己想从事的领域的时候,我会很自然地绕开任何ethical/privacy相关的东西,比如做ML research不碰ethical AI, 不碰differential privacy built in的ML model, 在Facebook选组绕开任何privacy相关的组等等。我曾短暂反思过这是为什么,我想我大概是”mad scientist“那种性格吧,认为privacy concern和ethical concern都是在拖慢的 technological advancement,也没有在为人类reach到星辰大海在服务。在这点上不想争论)。Anw,回到元宇宙的ethical concern上。很显然的一个问题就是,沉浸式元宇宙可能会让人堕落,in any way that could make sense。你可以成为一个300斤不运动的大胖子,同时在元宇宙里是个虚拟的健康滑雪运动员自我满足。这大概不是件好事。前段时间跟公司一位非常senior的同事聊天,他提到一个很有意思的观点: 这个世界贫富差距越来越大,你做的东西在初期打市场的时候,要么是为那贫穷的90%服务,要么就是为那富有的10%服务 (这是我的转述,大概是这个意思)。举个例子,元宇宙、抖音之类的产品就是让90%的穷人堕落的东西,特斯拉就是为10%的有钱人开发的产品。你选择为什么产品买单,一定程度上也说明了你是哪一类产品的目标用户(听完这段话之后我真的吓得立马把抖音删了)。有些东西,比如毒品,是naturally会让你堕落的,而类似抖音、元宇宙这样的产品则更加模棱两可。(当然啦,”怎么样算堕落“这个事情in itself又是一个说不清楚的话题。) 我不是说元宇宙一定会让人堕落,但是从刚才举的那个胖子的例子,至少说明元宇宙给了用户一个新的堕落的机会 (again,...
从亲密无间到形同陌路
人与人的关系奇妙得很。感情深刻的时候可以亲密无间恨不得分秒不离,淡了,就如形同陌路似乎从未相识。 形同陌路了,偶尔回想起曾经的如胶似漆,除了心底淡淡的难过,还有种莫名的感觉说不清楚。那个人好像还在眼前,却已经走得很远。好久没有听说你的消息,你还会想起我吗。我有那么多故事想说给你听,从我们不再说话那天。 于是遇到一个新的人,再次让彼此成为无话不说全世界最互相了解人,然后意识到你们的结局一定只会有两种:走到最后或者再也无法互相面对。
Humility, Gratitude and Compassion
(一) 教会里有一个教仪是“教长祝福“,有人视其为祝福,也有人视其为预言。当然也可不必赋予那么重的意义 --- 它是一封信,来自值得信任的智者。这封信的内容比较丰富,我每年都会读几次,每次读都会有不同的心得;有一段话,一直萦绕耳边、刻骨铭心: "I bless you with humility and gratitude, and that even as you are successful in your profession and career, you will remember to have compassion for those who are not as fortunate as you are." 三个关键词吧: Humility, Gratitude and Compassion. (二) 有一本书叫做"How Will You Measure Your Life",作者是哈佛商学院的一位教授,也是教会的一位教友。很多人都给我推荐过这本书,包括教会外的朋友。我大概是从前太小,对名字带有鸡汤意味的书都稍微有些抵触情绪,所以这些年来一直也没有去碰。前几天刚刚读完,觉得还是有许多蛮好的见解;不过倒也没有相见恨晚,现在读也刚刚好。 书里有提到“人生的意义”这种抽象的话题,也尝试从管理学的角度把它具体化。先不说我是否要完全按照书中的方式来思考人生意义;最起码这本书算是给我敲了一个警钟吧:借着这次重返学校的机会,再好好调整规划一下人生的目标吧。 (三) 小时候很愿意去到处宣扬自己所谓的人生规划,并且是很具体的那种,具体到xx岁要做什么事情。越长大,就越不愿意去设定具体的目标:可能是因为在经历某些小小的成就时并没有想象得知足,也可能是因为在经历过一些失望时懊悔为什么之前要设定那么高的预期。 我曾经和很多朋友说过,这些年来学过最重要的一个道理是”降低期待值“:如何降低自己对外界的期待,如何管理别人对自己的期待。这既是日渐成熟后的一丝智慧,也是青春渐逝对生活的逃避和妥协。...